115 lines
5.9 KiB
Markdown
115 lines
5.9 KiB
Markdown
|
|
---
|
|||
|
|
title: Limits Intro
|
|||
|
|
localeTitle: Límites de Introducción
|
|||
|
|
---
|
|||
|
|
## Límites
|
|||
|
|
|
|||
|
|
Decir que el límite de una función f (x) significa que ƒ (x) se puede hacer tan cerca como se desee de L haciendo que x sea lo suficientemente cerca, pero no igual, de p.
|
|||
|
|
|
|||
|
|
#### Ejemplo
|
|||
|
|
|
|||
|
|
Sea f (x) = x. Entonces el límite de f (x) cuando x tiende a 1 es igual a 1. Es decir, el valor de la función a medida que avanza sobre los valores de x, 0, luego 0.01, luego, 0.1, luego 0.5, y pasa a través de todos los valores en el eje x cada vez más cerca de 1, el valor de esa función f (x) = x tenderá a 1. A continuación, la gráfica de la función.
|
|||
|
|
|
|||
|
|
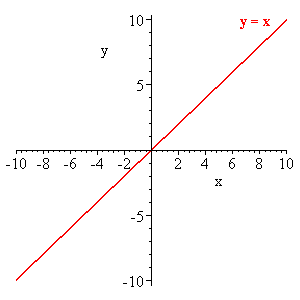
|
|||
|
|
|
|||
|
|
Cuando se dice que f (x) está muy cerca de L, pero no lo "toca", significa que su distancia es muy pequeña, de la misma manera, x tiende a a, pero no es igual a a, significa que x está a una distancia pequeña a partir de una. Para eso, se utiliza la definición de valor absoluto.
|
|||
|
|
|
|||
|
|
| f (x) - L | <ε, | x - a | <δ
|
|||
|
|
|
|||
|
|
Los símbolos, épsilon y delta, respectivamente, representan un número arbitrariamente pequeño.
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
La imagen de arriba indica lo siguiente: para cualquier pequeño ε> 0 (épsilon) que puede seleccionar, es posible dibujar una tira entre L + ε y L- ε, que sería la región amarilla o la franja horizontal. Luego, después de elegir ese épsilon, hay un cierto δ> 0 (delta), que puede determinarse, que le permite dibujar una franja vertical, al igual que la región rosa en el gráfico de arriba, la rosa, entre a + δ y un - δ. Ahora, si tomas cualquier x en la región rosa, es decir, alrededor de a, entonces este x estará más cerca de a que de a + δ y a - δ. O,
|
|||
|
|
|
|||
|
|
| x - a | <δ
|
|||
|
|
|
|||
|
|
Si ahora identifica el punto en el gráfico que da su elección de x, entonces este punto en el gráfico se encontrará en la intersección de la región rosa y amarilla. Esto significa que este valor de función f (x) estará más cerca de L que cualquiera de L + ε y L + ε. O,
|
|||
|
|
|
|||
|
|
| f (x) - L | <ε
|
|||
|
|
|
|||
|
|
Por lo tanto, si toma cualquier valor de x en la región rosa, entonces el gráfico para esos valores de x estará en la región amarilla.
|
|||
|
|
|
|||
|
|
De acuerdo, imagine la siguiente situación: usted y su amigo harán un viaje emocionante usando un mapa. Conducirás y tu amigo manejará el mapa por ti. Ahora, por cada pulgada en el mapa que te lea tu amigo, el auto se moverá, supongamos, 2 km o 1.24 millas, si lo prefieres. Tenga en cuenta que, a pesar de las unidades que estamos usando, solo para entenderlo, podemos escribir "su función" como:
|
|||
|
|
|
|||
|
|
f (pulgada) = 2km
|
|||
|
|
|
|||
|
|
Entonces, si tu amigo lee 2 pulgadas en el mapa, te habrás movido 4 km. Ustedes dos están cansados ahora y deciden descansar, pero tan inteligentes como usted y su amigo están, se preguntan:
|
|||
|
|
|
|||
|
|
* Oye, si tiendo a leer para ti, del mapa, las próximas 10 pulgadas, estamos cansados y tenemos que descansar de vez en cuando, así que no te leeré las diez pulgadas completas, pero estoy seguro de que Acérquese lo más posible, ¿cuánto cree que vamos a viajar?
|
|||
|
|
|
|||
|
|
Puedes pensar así:
|
|||
|
|
|
|||
|
|
* Sé que por cada centímetro que lees, conduzco 2 kilómetros! Entonces, si tiendes a leer 10 pulgadas ... hmm ... ¡posiblemente nos acerquemos lo más que podamos para conducir 20 kilómetros! No son exactamente los 20, pero ciertamente nos acercaremos mucho.
|
|||
|
|
|
|||
|
|
Esa es una forma de ilustrar este concepto, imagine que está caminando en el gráfico, la función es su "regla", la x es "cuánto tiene que caminar" y f (x) es el valor que realmente caminó, dado la regla que te han dado.
|
|||
|
|
|
|||
|
|
#### Propiedades
|
|||
|
|
|
|||
|
|
Considera que los límites de las funciones existen, entonces:
|
|||
|
|
|
|||
|
|
* **Suma**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
El límite de una suma es la suma de los límites.
|
|||
|
|
|
|||
|
|
Sea f (x) igual a x, f (x) = x y g (x) = 2x. Sea x para tender a 1. El límite:
|
|||
|
|
|
|||
|
|
lim (f (x) + g (x)) = lim f (x) + lim g (x) = lim x + lim 2x = 1 + 2 = 3
|
|||
|
|
|
|||
|
|
O lim (x + 2x) = lim (3x) = 3
|
|||
|
|
|
|||
|
|
* **Producto**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
El límite de un producto es el producto de los límites.
|
|||
|
|
|
|||
|
|
Considere la misma función en el ejemplo anterior, f (x) = x y g (x) = 2x. Y hace x tiende a 2, ahora.
|
|||
|
|
|
|||
|
|
lim (f (x) \* g (x)) = lim f (x) \* lim g (x) = 2 \* 4 = 8
|
|||
|
|
|
|||
|
|
O lim (x \* 2x) = lim (2x ^ 2) = 2 \* 4 = 8
|
|||
|
|
|
|||
|
|
* **Producto por una constante**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
Puedes “factorizar” una constante multiplicativa fuera de un límite.
|
|||
|
|
|
|||
|
|
De nuevo, supongamos que f (x) = x. El límite, dado x tiende a 5 ahora:
|
|||
|
|
|
|||
|
|
lim (10 \* x) = 10 lim (x) = 50
|
|||
|
|
|
|||
|
|
lim (10x) = 50
|
|||
|
|
|
|||
|
|
* **División**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
El límite de una división es la división de los límites.
|
|||
|
|
|
|||
|
|
Deje f (x) = 2x yg (x) = x + 1. Asegúrese de que la función que dividirá no sea cero. Hacer x tendiendo a 2, y tienes:
|
|||
|
|
|
|||
|
|
lim (2x / x) = lim 2x / lim x = 4/2 = 2
|
|||
|
|
|
|||
|
|
o lim (2x / 2) = lim 2 = 2. Esta es una función constante, por lo que no importa cuánto camines en el eje x, el valor siempre tenderá a ese valor en particular.
|
|||
|
|
|
|||
|
|
* **Poder**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
Si n es un entero
|
|||
|
|
|
|||
|
|
Sea f (x) igual a x + 1 y sea x tiende a 2. Supongamos el siguiente límite:
|
|||
|
|
|
|||
|
|
lim \[(x + 1)\] ^ 2 = (3) ^ 2 = 9
|
|||
|
|
|
|||
|
|
lim \[(x + 1)\] ^ 2 = lim (x ^ 2 + 2x + 1) = 9 (¡note que puede usar la propiedad de suma también!)
|
|||
|
|
|
|||
|
|
#### Más información:
|
|||
|
|
|
|||
|
|
[Notas y otros ejemplos.](http://tutorial.math.lamar.edu/Classes/CalcI/LimitsProperties.aspx)
|
|||
|
|
|
|||
|
|
[Introducción a los límites de la conferencia](https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-continuity/ab-limits-graphically/v/introduction-to-limits-hd)
|