freeCodeCamp/guide/english/mathematics/simpsons-rule/index.md

---
title: Simpson's Rule
---


# Simpson's Rule

In numerical analysis, Simpson's rule is a method for numerical integration <i>(numerical approximation of definite integrals)</i>.

Simpson's rule approximates the integration of the form,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim1.png)

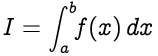
where, 
* `f(x)` is called the <i>integrand</i>
* `a` = lower limit of integration
* `b` = upper limit of integration

## Simpson's 1/3 Rule

<img src="https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim01.jpg" width="600"  alt="Simpson's Rule">

As shown in the diagram above, the integrand `f(x)` is approximated by a second order polynomial; the quadratic interpolant being `P(x)`.

The approximation follows,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim3.png)

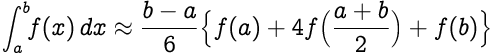
Replacing `(b-a)/2` as `h`, we get, 

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim4.png)

As you can see, there is a factor of `1/3` in the above expression. That's why, it is called <b>Simpson's 1/3 Rule</b>.

If a function is highly oscillatory or lacks derivatives at certain points, then the above rule may fail to produce accurate results. One common way of handling this problem is by breaking up the interval `[a,b]` into a number of small subintervals. Simpson's rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the <i>composite Simpson's rule</i>.

Suppose that the interval `[a,b]` is split up into `n` subintervals, with `n` being an even number. Then, the composite Simpson's rule is given by, 

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim7.png)

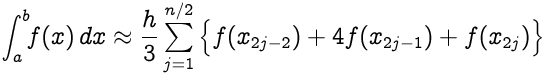
where <b>x<sub>j</sub> = a+jh</b> for <b>j = 0,1,...,n-1,n</b> with <b>h=(b-a)/n </b>; in particular, <b>x<sub>0</sub> = a</b> and <b>x<sub>n</sub> = b</b>.

#### Example:

<b>Approximate the value of the integral given below, taking n = 8. </b>

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim9.png)

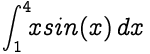
Implementation of Simpson's 1/3 Rule in C++ is as follows :

```cpp
#include<iostream>
#include<cmath>
using namespace std;

float f(float x)
{
	return x*sin(x);	//Define the function f(x)
}

float simpson(float a, float b, int n)
{
	float h, x[n+1], sum = 0;
	int j;
	h = (b-a)/n;
	
	x[0] = a;
	
	for(j=1; j<=n; j++)
	{
		x[j] = a + h*j;
	}
	
	for(j=1; j<=n/2; j++)
	{
		sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]);
	}
	
	return sum*h/3;
}

int main()
{
	float a,b,n;
	a = 1;		//Enter lower limit a
	b = 4;		//Enter upper limit b
	n = 8;		//Enter step-length n
	if (n%2 == 0)
		cout<<simpson(a,b,n)<<endl;
	else
		cout<<"n should be an even number";
	return 0;
}
```

## Simpson's 3/8 Rule

Simpson's 3/8 rule is similar to Simpson's 1/3 rule. The only difference is that, here, the interpolant is a cubic polynomial. The 3/8 rule is about twice as accurate as the 1/3 rule, but it uses one more function value.

Simpson's 3/8 rule states :

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim6.png)

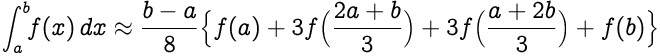
Replacing `(b-a)/3` as `h`, we get, 

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim5.png)

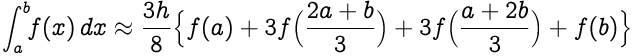
Simpson's 3/8 rule for n intervals (n should be a multiple of 3) :

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim8.png)

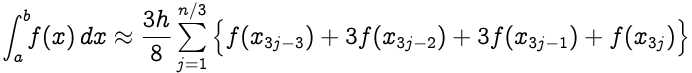
where <b>x<sub>j</sub> = a+jh</b> for <b>j = 0,1,...,n-1,n</b> with <b>h=(b-a)/n </b>; in particular, <b>x<sub>0</sub> = a</b> and <b>x<sub>n</sub> = b</b>.

### More Information:
1. <a href = "https://en.wikipedia.org/wiki/Simpson%27s_rule">Simpson's Rule</a>
2. <a href = "w3.gazi.edu.tr/~balbasi/mws_gen_int_txt_simpson13.pdf">Simpson's 1/3 Rule</a>