freeCodeCamp/guide/russian/mathematics/simpsons-rule/index.md

---
title: Simpson's Rule
localeTitle: Правило Симпсона
---
# Правило Симпсона

В численном анализе правило Симпсона является методом численного интегрирования _(численная аппроксимация определенных интегралов)_ .

Правило Симпсона аппроксимирует интегрирование формы,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim1.png)

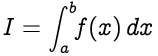
где,

*   `f(x)` называется _подынтегральным выражением_
*   `a` = нижний предел интеграции
*   `b` = верхний предел интеграции

## Правило Симпсона 1/3

![Simpson's Rule](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim01.jpg)

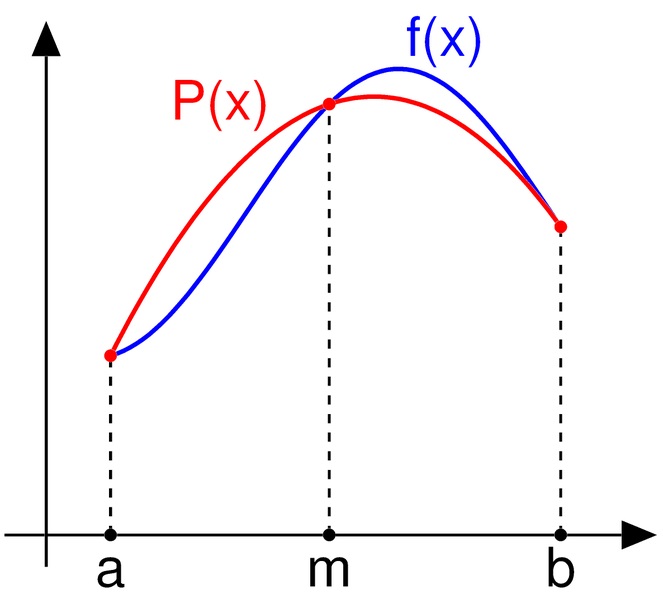
Как показано на диаграмме выше, подынтегральное выражение `f(x)` аппроксимируется полиномом второго порядка; квадратичным интерполятором является `P(x)` .

Далее следует приближение,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim3.png)

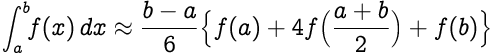
Заменяя `(ba)/2` как `h` , получаем,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim4.png)

Как вы можете видеть, в приведенном выше выражении есть коэффициент `1/3` . Вот почему это называется **Правилом 1/3 Симпсона** .

Если функция сильно осциллирует или не имеет производных в определенных точках, то приведенное выше правило может не дать точных результатов. Одним из распространенных способов решения этой проблемы является разбиение интервала `[a,b]` на несколько небольших подинтервалов. Затем правило Симпсона применяется к каждому подинтервалю, причем результаты суммируются для получения приближения интеграла по всему интервалу. Такой подход называется _составным правилом Симпсона_ .

Предположим, что отрезок `[a,b]` разбит на `n` подинтервалов, причем `n` - четное число. Затем составное правило Симпсона дается,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim7.png)

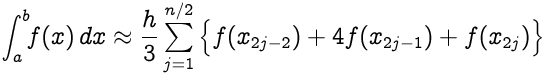
где **x j = a + jh** для **j = 0,1, ..., n-1, n** с **h = (ba) / n** ; в частности, **x 0 = a** и **x n = b** .

#### Пример:

**Приблизьте значение приведенного ниже интеграла, взяв n = 8.**

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim9.png)

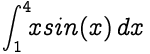
Реализация правила 1/3 Симпсона на C ++ заключается в следующем:

```cpp
#include<iostream> 
 #include<cmath> 
 using namespace std; 
 
 float f(float x) 
 { 
    return x*sin(x);    //Define the function f(x) 
 } 
 
 float simpson(float a, float b, int n) 
 { 
    float h, x[n+1], sum = 0; 
    int j; 
    h = (ba)/n; 
 
    x[0] = a; 
 
    for(j=1; j<=n; j++) 
    { 
        x[j] = a + h*j; 
    } 
 
    for(j=1; j<=n/2; j++) 
    { 
        sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]); 
    } 
 
    return sum*h/3; 
 } 
 
 int main() 
 { 
    float a,b,n; 
    a = 1;      //Enter lower limit a 
    b = 4;      //Enter upper limit b 
    n = 8;      //Enter step-length n 
    if (n%2 == 0) 
        cout<<simpson(a,b,n)<<endl; 
    else 
        cout<<"n should be an even number"; 
    return 0; 
 } 
```

## Правило 3/8 Симпсона

Правило 3/8 Симпсона аналогично правилу Симпсона 1/3. Единственное отличие состоит в том, что здесь интерполятор является кубическим многочленом. Правило 3/8 примерно в два раза точнее, чем правило 1/3, но оно использует еще одно значение функции.

Правило 3/8 Симпсона гласит:

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim6.png)

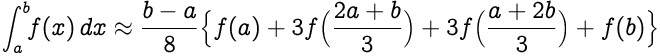
Заменяя `(ba)/3` как `h` , получаем,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim5.png)

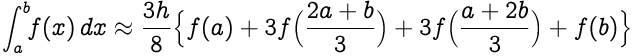
Правило 3/8 Симпсона для n интервалов (n должно быть кратно 3):

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim8.png)

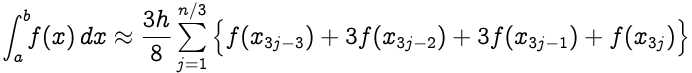
где **x j = a + jh** для **j = 0,1, ..., n-1, n** с **h = (ba) / n** ; в частности, **x 0 = a** и **x n = b** .

### Дополнительная информация:

1.  [Правило Симпсона](https://en.wikipedia.org/wiki/Simpson%27s_rule)
2.  [Правило Симпсона 1/3](w3.gazi.edu.tr/~balbasi/mws_gen_int_txt_simpson13.pdf)