---
title: Euler's Method
---
# Euler's Method
The Euler's method is a first-order numerical procedure for solving ordinary differential equations (ODE) with a given initial value.
## The General Initial Value Problem
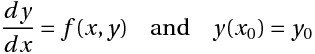
## Methodology
Euler's method uses the simple formula,
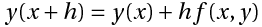
to construct the tangent at the point `x` and obtain the value of `y(x+h)`, whose slope is,
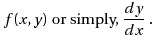
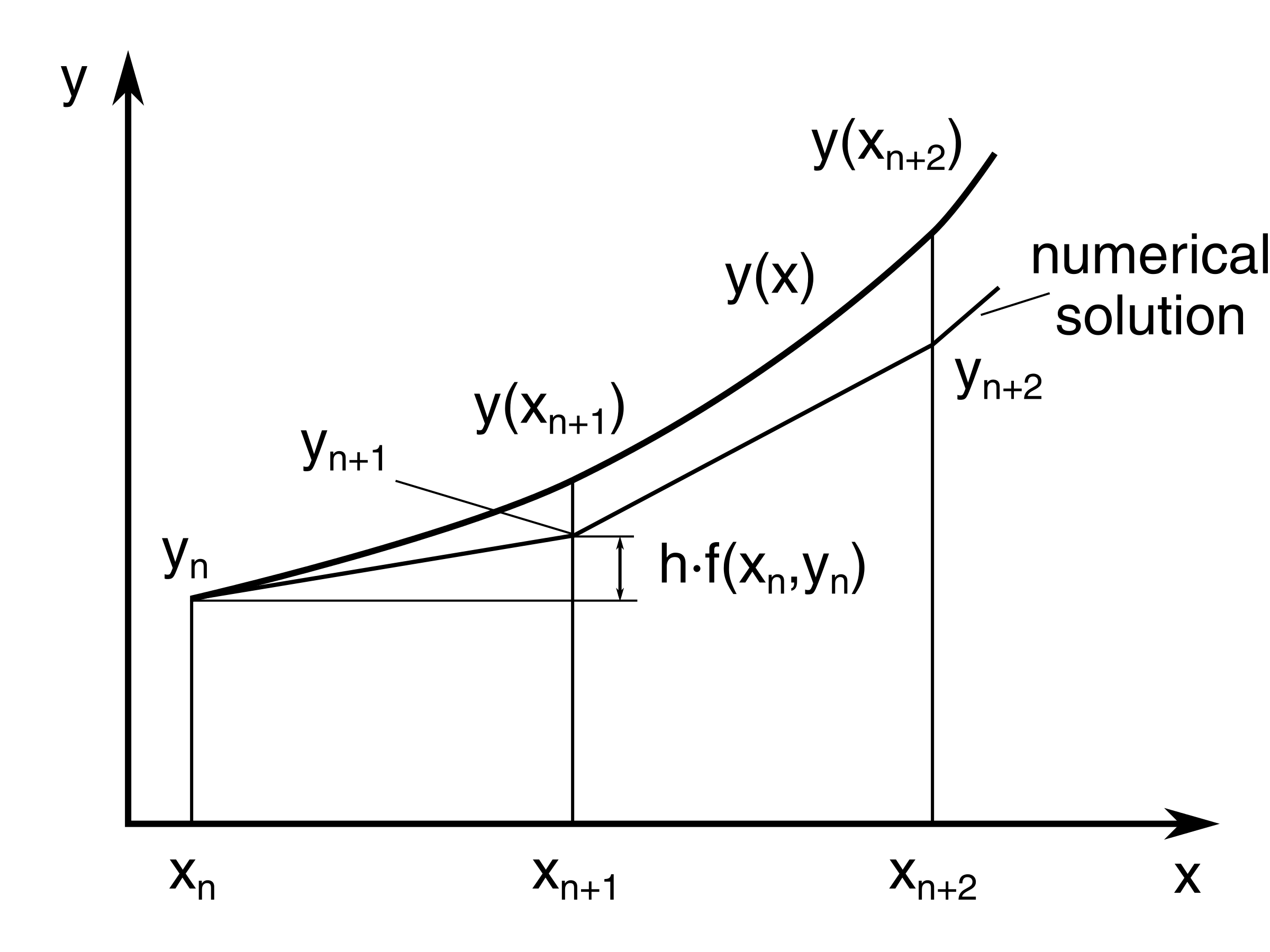 In Euler's method, you can approximate the curve of the solution by the tangent in each interval (that is, by a sequence of short line segments), at steps of `h`.
In general, if you use small step size, the accuracy of approximation increases.
## General Formula
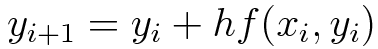

## Functional value at any point `b`, given by `y(b)`
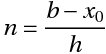
where,
* n = number of steps
* h = interval width (size of each step)
### Pseudocode

## Example
Find `y(1)`, given
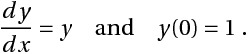
Solving analytically, the solution is y = ex and `y(1)`= `2.71828`. (Note: This analytic solution is just for comparing the accuracy.)
Using Euler's method, considering `h` = `0.2`, `0.1`, `0.01`, you can see the results in the diagram below.
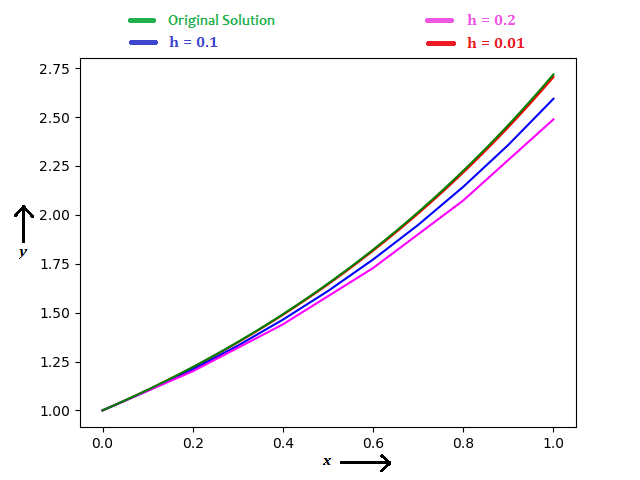
When `h` = `0.2`, `y(1)` = `2.48832` (error = 8.46 %)
When `h` = `0.1`, `y(1)` = `2.59374` (error = 4.58 %)
When `h` = `0.01`, `y(1)` = `2.70481` (error = 0.50 %)
You can notice, how accuracy improves when steps are small.
## More Information:
1. Numerical Methods for Solving Differential Equations
2. Euler's method
In Euler's method, you can approximate the curve of the solution by the tangent in each interval (that is, by a sequence of short line segments), at steps of `h`.
In general, if you use small step size, the accuracy of approximation increases.
## General Formula
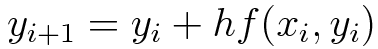

## Functional value at any point `b`, given by `y(b)`
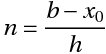
where,
* n = number of steps
* h = interval width (size of each step)
### Pseudocode

## Example
Find `y(1)`, given
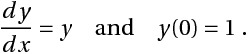
Solving analytically, the solution is y = ex and `y(1)`= `2.71828`. (Note: This analytic solution is just for comparing the accuracy.)
Using Euler's method, considering `h` = `0.2`, `0.1`, `0.01`, you can see the results in the diagram below.

When `h` = `0.2`, `y(1)` = `2.48832` (error = 8.46 %)
When `h` = `0.1`, `y(1)` = `2.59374` (error = 4.58 %)
When `h` = `0.01`, `y(1)` = `2.70481` (error = 0.50 %)
You can notice, how accuracy improves when steps are small.
## More Information:
1. Numerical Methods for Solving Differential Equations
2. Euler's method
 In Euler's method, you can approximate the curve of the solution by the tangent in each interval (that is, by a sequence of short line segments), at steps of `h`.
In general, if you use small step size, the accuracy of approximation increases.
## General Formula
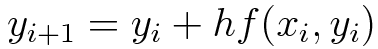

## Functional value at any point `b`, given by `y(b)`
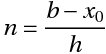
where,
* n = number of steps
* h = interval width (size of each step)
### Pseudocode

## Example
Find `y(1)`, given
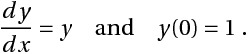
Solving analytically, the solution is y = ex and `y(1)`= `2.71828`. (Note: This analytic solution is just for comparing the accuracy.)
Using Euler's method, considering `h` = `0.2`, `0.1`, `0.01`, you can see the results in the diagram below.

When `h` = `0.2`, `y(1)` = `2.48832` (error = 8.46 %)
When `h` = `0.1`, `y(1)` = `2.59374` (error = 4.58 %)
When `h` = `0.01`, `y(1)` = `2.70481` (error = 0.50 %)
You can notice, how accuracy improves when steps are small.
## More Information:
1. Numerical Methods for Solving Differential Equations
2. Euler's method
In Euler's method, you can approximate the curve of the solution by the tangent in each interval (that is, by a sequence of short line segments), at steps of `h`.
In general, if you use small step size, the accuracy of approximation increases.
## General Formula
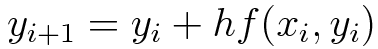

## Functional value at any point `b`, given by `y(b)`
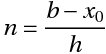
where,
* n = number of steps
* h = interval width (size of each step)
### Pseudocode

## Example
Find `y(1)`, given
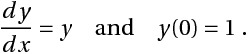
Solving analytically, the solution is y = ex and `y(1)`= `2.71828`. (Note: This analytic solution is just for comparing the accuracy.)
Using Euler's method, considering `h` = `0.2`, `0.1`, `0.01`, you can see the results in the diagram below.

When `h` = `0.2`, `y(1)` = `2.48832` (error = 8.46 %)
When `h` = `0.1`, `y(1)` = `2.59374` (error = 4.58 %)
When `h` = `0.01`, `y(1)` = `2.70481` (error = 0.50 %)
You can notice, how accuracy improves when steps are small.
## More Information:
1. Numerical Methods for Solving Differential Equations
2. Euler's method