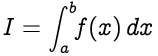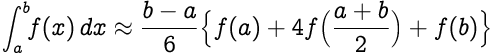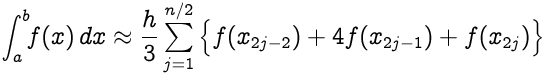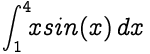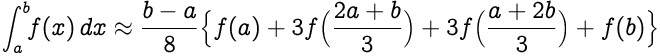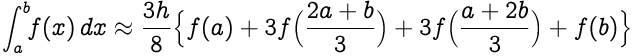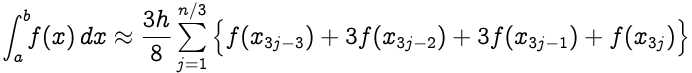4.5 KiB

Raw Blame History

title	localeTitle
Simpson's Rule	حكم سيمبسون

حكم سيمبسون

في التحليل العددي ، تعتبر قاعدة سيمبسون طريقة للتكامل العددي (التقريب الرقمي للاندماجات المحددة) .

تقارب قاعدة سيمبسون تكامل النموذج ،

أين،

f(x) يسمى integrand
a = الحد الأدنى للتكامل
b = الحد الأعلى للتكامل

حكم سيمبسون 1/3

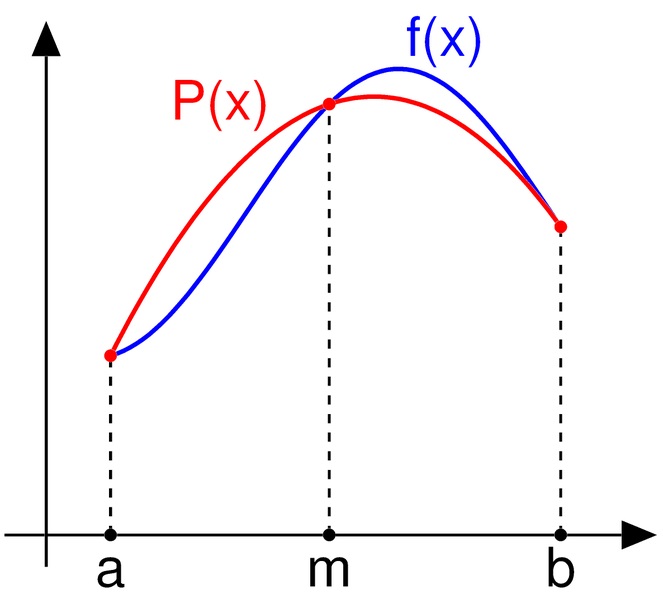
كما هو موضح في الرسم البياني أعلاه ، يقترب الرقم integre f(x) من متعدد الحدود من الدرجة الثانية ؛ يكون interpolant التربيعي P(x) .

يتبع التقريب ،

استبدال (ba)/2 as h ، we get،

كما ترى ، هناك عامل 1/3 في التعبير أعلاه. لهذا السبب ، يطلق عليه اسم قاعدة سيمبسون 1/3 .

إذا كانت الوظيفة متذبذبة للغاية أو تفتقر إلى المشتقات في نقاط معينة ، فقد تفشل القاعدة المذكورة أعلاه في الحصول على نتائج دقيقة. تتمثل إحدى الطرق الشائعة لمعالجة هذه المشكلة في تقسيم الفاصل الزمني [a,b] إلى عدد من subintervals الصغيرة. ثم يتم تطبيق قاعدة سيمبسون على كل فئة فرعية ، مع جمع النتائج لإنتاج تقريب للتكامل خلال الفترة الزمنية بأكملها. يطلق على هذا النوع من النهج قاعدة سيمبسون المركبة .

لنفترض أن الفاصل [a,b] مقسم إلى n subintervals ، مع n رقم زوجي. ثم ، يتم إعطاء القاعدة المركبة سيمبسون من قبل ،

حيث x j = a + jh لـ j = 0،1،…، n-1، n with h = (ba) / n ؛ على وجه الخصوص ، x 0 = a و x n = b .

مثال:

تقريبًا قيمة التكامل المضمن أدناه ، مع أخذ n = 8.

تنفيذ قاعدة 1/3 من Simpson في C ++ كما يلي:

`#include #include using namespace std;

float f(float x) { return x*sin(x); //Define the function f(x) }

float simpson(float a, float b, int n) { float h, x[n+1], sum = 0; int j; h = (ba)/n;

x[0] = a; 

for(j=1; j<=n; j++) 
{ 
    x[j] = a + h*j; 
} 

for(j=1; j<=n/2; j++) 
{ 
    sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]); 
} 

return sum*h/3;

}

int main() { float a,b,n; a = 1; //Enter lower limit a b = 4; //Enter upper limit b n = 8; //Enter step-length n if (n%2 == 0) cout<<simpson(a,b,n)<<endl; else cout<<"n should be an even number"; return 0; } `

سيمبسون 3/8 القاعدة

تشبه قاعدة 3/8 لـ Simpson قاعدة 1/3 الخاصة بـ Simpson. والفرق الوحيد هو ، هنا ، أن interpolant هو متعدد الحدود التكعيبية. قاعدة 3/8 تقارب ضعف دقة القاعدة 1/3 ، ولكنها تستخدم قيمة دالة واحدة أكثر.

تنص قواعد 3/8 لـ Simpson على ما يلي:

استبدال (ba)/3 as h ، we get،

قاعدة 3/8 لـ Simpson للفترات n (يجب أن تكون n مضاعفات 3):