freeCodeCamp/guide/spanish/mathematics/simpsons-rule/index.md

---
title: Simpson's Rule
localeTitle: Regla de simpson
---
# Regla de simpson

En el análisis numérico, la regla de Simpson es un método para la integración _numérica (aproximación numérica de integrales definidas)_ .

La regla de Simpson se aproxima a la integración de la forma,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim1.png)

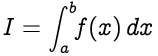
dónde,

*   `f(x)` se llama _integrand_
*   `a` = límite inferior de integración
*   `b` = límite superior de integración

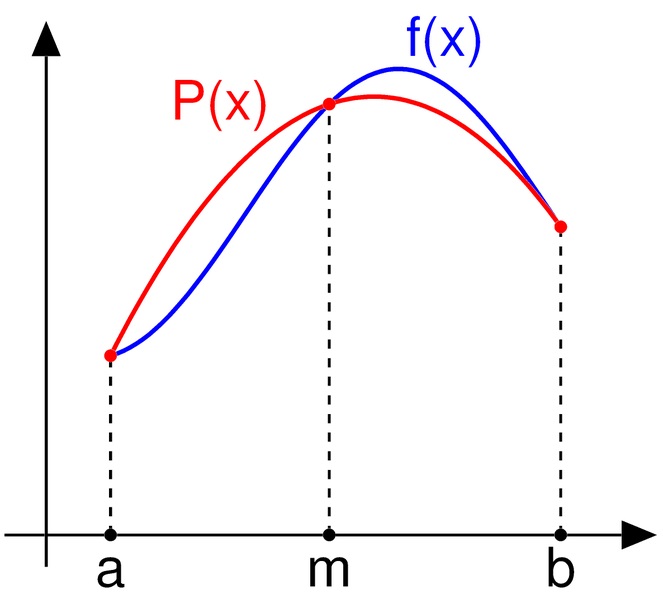
## Regla 1/3 de Simpson

![Simpson's Rule](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim01.jpg)

Como se muestra en el diagrama anterior, el integrando `f(x)` se aproxima mediante un polinomio de segundo orden; siendo el interpolante cuadrático `P(x)` .

La aproximación sigue,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim3.png)

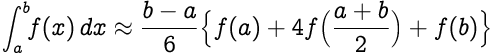
Reemplazando `(ba)/2` como `h` , obtenemos,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim4.png)

Como puede ver, hay un factor de `1/3` en la expresión anterior. Por eso, se llama **la regla 1/3 de Simpson** .

Si una función es altamente oscilatoria o carece de derivados en ciertos puntos, entonces la regla anterior puede no producir resultados precisos. Una forma común de manejar este problema es dividiendo el intervalo `[a,b]` en varios subintervalos pequeños. La regla de Simpson se aplica a cada subintervalo, y los resultados se suman para producir una aproximación de la integral en todo el intervalo. Este tipo de enfoque se denomina la _regla de Simpson compuesta_ .

Supongamos que el intervalo `[a,b]` se divide en `n` subintervalos, siendo `n` un número par. Entonces, la regla compuesta de Simpson está dada por,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim7.png)

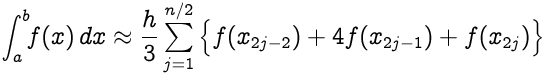
donde **x j = a + jh** para **j = 0,1,…, n-1, n** con **h = (ba) / n** ; en particular, **x 0 = a** y **x n = b** .

#### Ejemplo:

**Aproxime el valor de la integral dada a continuación, tomando n = 8.**

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim9.png)

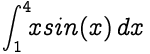
La implementación de la regla 1/3 de Simpson en C ++ es la siguiente:

```cpp
#include<iostream> 
 #include<cmath> 
 using namespace std; 
 
 float f(float x) 
 { 
    return x*sin(x);    //Define the function f(x) 
 } 
 
 float simpson(float a, float b, int n) 
 { 
    float h, x[n+1], sum = 0; 
    int j; 
    h = (ba)/n; 
 
    x[0] = a; 
 
    for(j=1; j<=n; j++) 
    { 
        x[j] = a + h*j; 
    } 
 
    for(j=1; j<=n/2; j++) 
    { 
        sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]); 
    } 
 
    return sum*h/3; 
 } 
 
 int main() 
 { 
    float a,b,n; 
    a = 1;      //Enter lower limit a 
    b = 4;      //Enter upper limit b 
    n = 8;      //Enter step-length n 
    if (n%2 == 0) 
        cout<<simpson(a,b,n)<<endl; 
    else 
        cout<<"n should be an even number"; 
    return 0; 
 } 
```

## Regla 3/8 de Simpson

La regla de 3/8 de Simpson es similar a la regla de 1/3 de Simpson. La única diferencia es que, aquí, el interpolante es un polinomio cúbico. La regla 3/8 es aproximadamente el doble de precisa que la regla 1/3, pero utiliza un valor de función más.

La regla 3/8 de Simpson dice:

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim6.png)

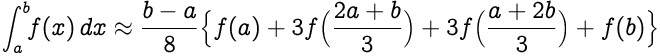
Reemplazando `(ba)/3` como `h` , obtenemos,

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim5.png)

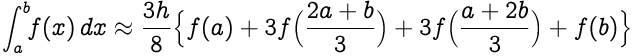
La regla 3/8 de Simpson para n intervalos (n debe ser un múltiplo de 3):

![](https://raw.githubusercontent.com/pranabendra/articles/master/Simpson-Method/sim8.png)

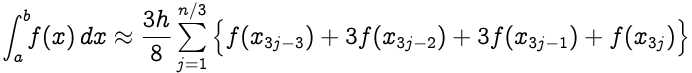
donde **x j = a + jh** para **j = 0,1,…, n-1, n** con **h = (ba) / n** ; en particular, **x 0 = a** y **x n = b** .

### Más información:

1.  [Regla de simpson](https://en.wikipedia.org/wiki/Simpson%27s_rule)
2.  [Regla 1/3 de Simpson](w3.gazi.edu.tr/~balbasi/mws_gen_int_txt_simpson13.pdf)