118 lines
5.4 KiB
Markdown
118 lines
5.4 KiB
Markdown
---
|
|
title: Limits Intro
|
|
---
|
|
|
|
## Limits
|
|
|
|
To say the limit of a function f(x) means that ƒ(x) can be made as close as desired to L by making x close enough, but not equal, to p.
|
|
|
|
#### Example
|
|
|
|
Let f(x) = x. Then the limit of f(x) as x tends to 1 is equal to 1. That is, the value of the function as you walk on values of x, 0, then 0.01, then, 0.1, then 0.5, and passing through all the values on the x-axis getting closer and closer to 1, the value of that function f(x) = x will tend to 1. Bellow, the graph of the function.
|
|
|
|
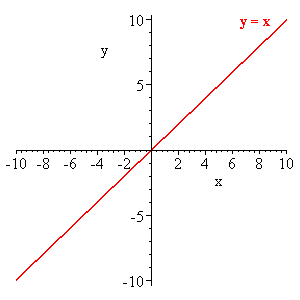
|
|
|
|
When one says that f(x) is very close to L, but does not "touch" it, means that their distance is very small, likewise, x tends to a, but not equal to a, means x is at a small distance from a. For that, the definition of absolute value is used.
|
|
|
|
|f(x) - L| < ε , |x - a|< δ
|
|
|
|
The symbols, epsilon and delta, respectively, represent an arbitrarily small number.
|
|
|
|

|
|
|
|
The picture above tells the following: for any small ε>0 (epsilon) you may pick, is possible to draw a strip between L+ ε and L- ε, that would the yellow region, or the horizontal strip. Then, after choosing that epsilon, there is a certain δ>0 (delta), which can be determined, that allows you to draw a vertical strip, just like the pink region on the graph above, the pink one, between a + δ and a - δ. Now, if you take any x in the pink region, that is around a, then this x will be closer to a than either of a + δ and a - δ. Or,
|
|
|
|
|x - a|< δ
|
|
|
|
If you now identify the point on the graph that your choice of x gives, then this point on the graph will lie in the intersection of the pink and yellow region. This means that this function value f(x) will be closer to L than either of L + ε and L + ε . Or,
|
|
|
|
|f(x) - L| < ε
|
|
|
|
So, if you take any value of x in the pink region then the graph for those values of x will lie in the yellow region.
|
|
|
|
Okay, imagine the following situation: you and your friend will make an exciting travel using a map. You will drive and your friend will handle the map for you. Now, for each inch in the map your friend reads to you, the car will move, suppose, 2Km, or 1.24 miles, if you prefer. Notice that, despite units we are using, just for the matter of understanding it, we could write "your function" as:
|
|
|
|
f(inch) = 2km
|
|
|
|
So, if your friend reads 2 inches on the map, you'll have moved 4km. You two are tired now and decide to rest, but smart as you and your friend are, you two wonder:
|
|
|
|
- Hey, if I tend to read for you, from the map, the next 10 inches, we are tired, and have to rest every now and then, so I wont read you the whole ten inches, but I'm sure I'll get as close as we can possibly get, how much do you think we will travel?
|
|
|
|
You can think like this:
|
|
|
|
- I know that for each inch you read, I drive 2 kilometers! so, if you tend to read 10 inches...hmm... we will possibly get as close as we can to drive 20 kilometers! Not exactly the 20, but we'll certaily get very very close.
|
|
|
|
That is a way to illustrate this concept, imagine you are walking on the graph, the function is your "rule", the x is "how much you have to walk", and f(x) is the value you actually walked, given the rule you've been given.
|
|
|
|
#### Properties
|
|
|
|
Consider that the limits of the functions exist, then:
|
|
|
|
* **Sum**
|
|
|
|

|
|
|
|
The limit of a sum is the sum of the limits.
|
|
|
|
Let f(x) be equal to x, f(x) = x and g(x) = 2x. Let x to tend to 1. The limit:
|
|
|
|
lim (f(x) + g(x)) = lim f(x) + lim g(x ) = lim x + lim 2x = 1 + 2 = 3
|
|
|
|
Or lim (x + 2x) = lim (3x) = 3
|
|
|
|
* **Product**
|
|
|
|

|
|
|
|
The limit of a product is the product of the limits.
|
|
|
|
Consider the same function on the previous example, f(x) = x and g(x) = 2x. And make x tends to 2, now.
|
|
|
|
lim(f(x) * g(x)) = lim f(x) * lim g(x) = 2 * 4 = 8
|
|
|
|
Or lim(x * 2x) = lim (2x^2) = 2 * 4 = 8
|
|
|
|
* **Product by a constant**
|
|
|
|

|
|
|
|
You can “factor” a multiplicative constant out of a limit.
|
|
|
|
Again, assume f(x) = x. The limit, given x tending to 5 now:
|
|
|
|
lim (10 * x) = 10 lim (x) = 50
|
|
|
|
lim (10x) = 50
|
|
|
|
* **Division**
|
|
|
|

|
|
|
|
The limit of a division is the division of the limits.
|
|
|
|
Let f(x) = 2x and g(x) = x + 1. Make sure the the function you'll devide by is not zero. make x tending to 2, and you have:
|
|
|
|
lim ( 2x / x ) = lim 2x / lim x = 4 / 2 = 2
|
|
|
|
or lim (2x / 2) = lim 2 = 2. This is a constant function, so no matter how much you walk alonf the x-axis, the value will always tend to that one particular value.
|
|
|
|
* **Power**
|
|
|
|

|
|
|
|
If n is an integer.
|
|
|
|
Let f(x) be equal to x + 1 and let x tends to 2. Assume the following limit:
|
|
|
|
lim [(x + 1)]^2 = (3)^2 = 9
|
|
|
|
lim [(x + 1)]^2 = lim (x^2 + 2x + 1) = 9 (notice you can use the sum property as well!)
|
|
|
|
|
|
#### More Information:
|
|
[Notes and further examples](http://tutorial.math.lamar.edu/Classes/CalcI/LimitsProperties.aspx)
|
|
|
|
[Intro To limits lecture](https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-continuity/ab-limits-graphically/v/introduction-to-limits-hd)
|
|
|
|
|