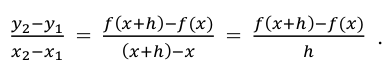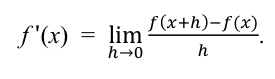3.2 KiB
| title |
|---|
| Derivatives |
Derivatives
The derivative is the instantaneous rate of change of a function, or the rate of change of a function at any particular instant in time. The derivative is a tool of calculus and you can determine it by taking a limit.
You can understand the concept of derivative by comparing it with the concept of slope (the average rate of change) in algebra.
Let’s take a look at an example:
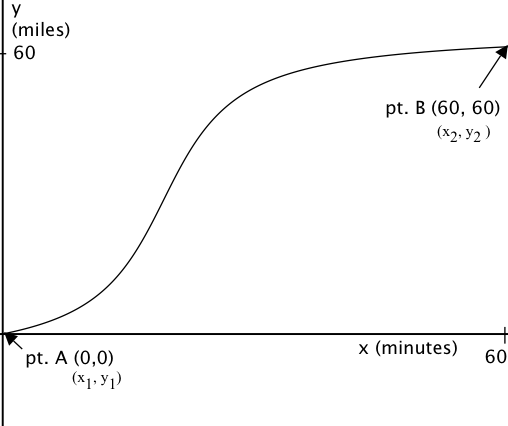
You decide to drive from San Francisco to Santa Rosa, California – a distance of roughly 60 miles. You make the drive in one hour; thus, your average rate of change (speed) is 60 miles per hour.
But, you did not travel at a rate of 60 miles per hour for each instant of your trip. You started off slower, then increased your speed and varied it along the way, and then slowed down to a full stop when you arrived at your destination.
Let’s take a look at the graph of your trip, with the x-axis representing time (in minutes) and the y-axis representing distance (in miles). Pt. A represents San Francisco, with coordinates (0, 0) and pt. B represents Santa Rosa, with coordinates (60, 60). The curved line represents your location, in space and time, as you traveled from San Francisco to Santa Rosa.
You can determine the average speed (rate of the change in distance per time) of your trip by taking the algebra slope (“rise over run”):
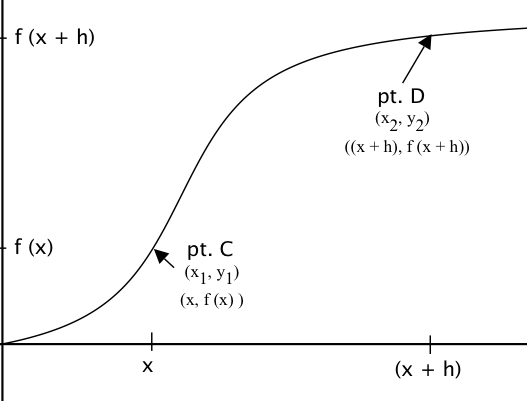
Using the same graph, you can pick any two points, C (x1, y1) and D (x2, y2) and find the slope between them. Moreover, you can label each point using function notation, such that (x1, y1) becomes (x, f(x)) and (x2, y2) becomes ((x + h), f(x + h)), with h being the horizontal distance that pt. D is from pt. C:
The slope from pt. C to pt. D is:
The expression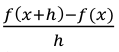 
is called the difference quotient and you can use it to find the average rate of change from any point on a graph to any other point a horizontal distance of h units away.
To convert the average rate of change (the slope) to an instantaneous rate of change (the derivative, notated as f (x)), you take the limit of the difference quotient:
This is the formal definition of the derivative and means that you are taking the distance h and shrinking it down to an infinitesimally small amount. You still have a slope, but its end-points are infinitesimally close to each other. So close, in fact, that they appear as one point, or as one instant, in time.
Since a line tangent to a point on a graph intersects the graph at only one point, the derivative is also defined as the slope of the tangent line to any point on a graph. In the example of the above graph, the derivative of each point is the instantaneous speed at which you are traveling.
Derivatives have a wide range of applications and are used in physics, engineering, economics, and other disciplines.