115 lines
5.8 KiB
Markdown
115 lines
5.8 KiB
Markdown
---
|
||
title: Limits Intro
|
||
localeTitle: Limites Intro
|
||
---
|
||
## Limites
|
||
|
||
Dizer que o limite de uma função f (x) significa que ƒ (x) pode ser feito o mais próximo possível de L, fazendo x aproximar o suficiente, mas não igual, de p.
|
||
|
||
#### Exemplo
|
||
|
||
Seja f (x) = x. Então o limite de f (x) como x tende a 1 é igual a 1. Ou seja, o valor da função enquanto você anda sobre valores de x, 0, então 0.01, depois, 0.1, depois 0.5, e passando por todos os valores no eixo x aproximando-se cada vez mais de 1, o valor dessa função f (x) = x tenderá a 1. Abaixo, o gráfico da função.
|
||
|
||
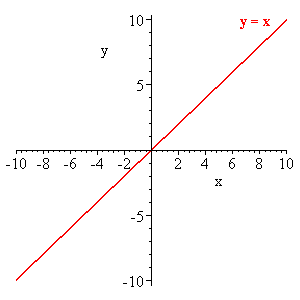
|
||
|
||
Quando alguém diz que f (x) está muito próximo de L, mas não "toca", significa que sua distância é muito pequena, da mesma forma, x tende a, mas não é igual a a, significa que x está a uma distância pequena a partir de um. Para isso, a definição de valor absoluto é usada.
|
||
|
||
| f (x) - L | <ε, | x - a | <δ
|
||
|
||
Os símbolos epsilon e delta, respectivamente, representam um número arbitrariamente pequeno.
|
||
|
||

|
||
|
||
A figura acima diz o seguinte: para qualquer pequeno ε> 0 (epsilon) que você possa escolher, é possível desenhar uma faixa entre L + ε e L- ε, que seria a região amarela, ou a faixa horizontal. Então, depois de escolher esse épsilon, existe um certo δ> 0 (delta), que pode ser determinado, que permite desenhar uma tira vertical, assim como a região rosa no gráfico acima, a rosa, entre a + δ e a - δ. Agora, se você pegar qualquer x na região rosa, isto é ao redor de a, então este x estará mais próximo de a que + a + δ e a - δ. Ou,
|
||
|
||
| x - a | <δ
|
||
|
||
Se você agora identificar o ponto no gráfico que a sua escolha de x dá, então este ponto no gráfico estará na interseção da região rosa e amarela. Isto significa que este valor de função f (x) estará mais próximo de L do que de L + ε e L + ε. Ou,
|
||
|
||
| f (x) - L | <ε
|
||
|
||
Então, se você pegar qualquer valor de x na região rosa, então o gráfico para esses valores de x estará na região amarela.
|
||
|
||
Ok, imagine a seguinte situação: você e seu amigo farão uma viagem emocionante usando um mapa. Você vai dirigir e seu amigo vai lidar com o mapa para você. Agora, para cada centímetro no mapa que seu amigo lê para você, o carro vai se mover, suponha, 2 km ou 1,24 milhas, se você preferir. Observe que, apesar das unidades que estamos usando, apenas para entender, poderíamos escrever "sua função" como:
|
||
|
||
f (polegada) = 2 km
|
||
|
||
Então, se seu amigo ler 2 polegadas no mapa, você terá movido 4 km. Vocês dois estão cansados agora e decidem descansar, mas espertos como você e seu amigo são, vocês dois se perguntam:
|
||
|
||
* Ei, se eu tender a ler para você, no mapa, os próximos 10 polegadas, estamos cansados, e temos que descansar de vez em quando, então eu não vou te ler os dez polegadas inteiros, mas tenho certeza que vou chegar o mais perto possível, quanto você acha que vamos viajar?
|
||
|
||
Você pode pensar assim:
|
||
|
||
* Eu sei que para cada polegada que você lê, dirijo 2 quilômetros! então, se você tende a ler 10 polegadas… hmm… nós possivelmente chegaremos o mais perto possível para dirigir 20 quilômetros! Não exatamente os 20, mas certamente ficaremos muito próximos.
|
||
|
||
Essa é uma maneira de ilustrar esse conceito, imagine que você está andando no gráfico, a função é sua "regra", o x é "quanto você tem que andar", e f (x) é o valor que você realmente andou, dado a regra que você recebeu.
|
||
|
||
#### Propriedades
|
||
|
||
Considere que os limites das funções existem, então:
|
||
|
||
* **Soma**
|
||
|
||

|
||
|
||
O limite de uma soma é a soma dos limites.
|
||
|
||
Seja f (x) igual a x, f (x) = x e g (x) = 2x. Deixe x tender para 1. O limite:
|
||
|
||
lim (f (x) + g (x)) = lim f (x) + lim g (x) = lim x + lim 2x = 1 + 2 = 3
|
||
|
||
Ou lim (x + 2x) = lim (3x) = 3
|
||
|
||
* **produtos**
|
||
|
||

|
||
|
||
O limite de um produto é o produto dos limites.
|
||
|
||
Considere a mesma função no exemplo anterior, f (x) = x e g (x) = 2x. E faça x tende a 2, agora.
|
||
|
||
lim (f (x) \* g (x)) = lim f (x) \* lim g (x) = 2 \* 4 = 8
|
||
|
||
Ou lim (x \* 2x) = lim (2x ^ 2) = 2 \* 4 = 8
|
||
|
||
* **Produto por uma constante**
|
||
|
||

|
||
|
||
Você pode "fatorar" uma constante multiplicativa fora de um limite.
|
||
|
||
Novamente, assuma f (x) = x. O limite, dado x tendendo a 5 agora:
|
||
|
||
lim (10 x) = 10 lim (x) = 50
|
||
|
||
lim (10x) = 50
|
||
|
||
* **Divisão**
|
||
|
||

|
||
|
||
O limite de uma divisão é a divisão dos limites.
|
||
|
||
Seja f (x) = 2x e g (x) = x + 1. Certifique-se de que a função a ser usada não seja zero. faça x tendendo para 2 e você tem:
|
||
|
||
lim (2x / x) = lim 2x / lim x = 4/2 = 2
|
||
|
||
ou lim (2x / 2) = lim 2 = 2. Esta é uma função constante, portanto, não importa o quanto você ande sozinho no eixo x, o valor tenderá sempre a esse valor específico.
|
||
|
||
* **Poder**
|
||
|
||

|
||
|
||
Se n é um inteiro.
|
||
|
||
Seja f (x) igual a x + 1 e seja x tende a 2. Suponha o seguinte limite:
|
||
|
||
lim \[(x + 1)\] ^ 2 = (3) ^ 2 = 9
|
||
|
||
lim \[(x + 1)\] ^ 2 = lim (x ^ 2 + 2x + 1) = 9 (observe que você também pode usar a propriedade sum!)
|
||
|
||
#### Mais Informações:
|
||
|
||
[Notas e outros exemplos](http://tutorial.math.lamar.edu/Classes/CalcI/LimitsProperties.aspx)
|
||
|
||
[Introdução para limitar a palestra](https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-continuity/ab-limits-graphically/v/introduction-to-limits-hd) |