115 lines
7.4 KiB
Markdown
115 lines
7.4 KiB
Markdown
---
|
|
title: Limits Intro
|
|
localeTitle: حدود المقدمة
|
|
---
|
|
## حدود
|
|
|
|
ﻟﻘول أن ﺣد اﻟوظﯾﻔﺔ f (x) ﯾﻌﻧﻲ أن ƒ (x) ﯾﻣﮐن إﺟراؤھﺎ ﺑﺎﻟﻘرب ﻣن اﻟﻣرﻏوﺑﺔ إﻟﯽ L ﻋن طرﯾق ﺟﻌل x ﻣﻐﻟﻘًﺎ ﺑﻣﺎ ﯾﮐﻔﻲ ، وﻟﮐن ﻟﯾس ﻣﺳﺎوﯾﺎً ، إﻟﯽ p.
|
|
|
|
#### مثال
|
|
|
|
دع f (x) = x. عندئذ يكون حد f (x) حيث أن x يميل إلى 1 يساوي 1. وهذا يعني ، قيمة الدالة أثناء المشي على قيم x ، 0 ، ثم 0.01 ، ثم ، 0.1 ، ثم 0.5 ، وتمرير كل القيم على x-axis تقترب وأقرب إلى 1 ، فإن قيمة هذه الدالة f (x) = x ستميل إلى 1. رفع الصوت ، الرسم البياني للوظيفة.
|
|
|
|
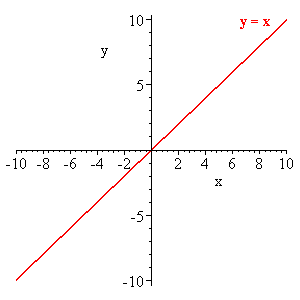
|
|
|
|
عندما يقول المرء أن f (x) قريب جداً من L ، لكنه لا "يلمس" ، يعني أن المسافة صغيرة جداً ، وبالمثل ، x يميل إلى a ، ولكن ليس مساوياً لـ ، يعني x على مسافة صغيرة من. لذلك ، يتم استخدام تعريف القيمة المطلقة.
|
|
|
|
| f (x) - L | <ε، | x - a | <δ
|
|
|
|
تمثل الرموز ، epsilon والدلتا ، على التوالي ، عدد صغير بشكل تعسفي.
|
|
|
|

|
|
|
|
توضح الصورة أعلاه ما يلي: لأي small> 0 صغير (epsilon) قد تختار ، من الممكن رسم شريط بين L + ε و L- ε ، من شأنه أن يكون المنطقة الصفراء ، أو الشريط الأفقي. بعد ذلك ، بعد اختيار ذلك epsilon ، هناك δ> 0 (دلتا) معينة ، والتي يمكن تحديدها ، والتي تتيح لك رسم شريط رأسي ، تمامًا مثل المنطقة الوردية على الرسم البياني أعلاه ، اللون الوردي ، بين + δ و- δ. الآن ، إذا أخذت أي x في المنطقة الوردية ، أي حول ، فستكون هذه القيمة x أقرب إلى أي من a + δ و a - δ. أو،
|
|
|
|
| x - a | <δ
|
|
|
|
إذا حددت الآن النقطة على الرسم البياني التي يعطيها اختيارك لـ x ، فإن هذه النقطة في الرسم البياني ستقع في تقاطع المنطقة الوردية والأصفر. وهذا يعني أن قيمة هذه الدالة f (x) ستكون أقرب إلى L من أي من L + ε و L + ε. أو،
|
|
|
|
| f (x) - L | <ε
|
|
|
|
لذا ، إذا أخذت أي قيمة x في المنطقة الوردية ، فسيظهر الرسم البياني لهذه القيم لـ x في المنطقة الصفراء.
|
|
|
|
حسنًا ، تخيل الموقف التالي: ستجعلك أنت وصديقك رحلة مثيرة باستخدام خريطة. سوف تقود وسيعالج صديقك الخريطة. الآن ، لكل بوصة في الخريطة يقرأ لك صديقك ، ستتحرك السيارة ، لنفترض ، 2 كم ، أو 1.24 ميل ، إذا كنت تفضل ذلك. لاحظ أنه على الرغم من الوحدات التي نستخدمها ، لمجرد فهمها ، يمكننا كتابة "وظيفتك" على النحو التالي:
|
|
|
|
f (بوصة) = 2 كم
|
|
|
|
لذلك ، إذا قرأ صديقك بوصتين على الخريطة ، فسيتم تحريكك لمسافة 4 كم. أنتما متعبان الآن وتقرران أن تستريح ، لكنك ذكي كما أنت وصديقك ، فأنت تساءلان:
|
|
|
|
* مهلا ، إذا كنت أميل إلى القراءة بالنسبة لك ، من الخريطة ، وبوصة 10 بوصات ، ونحن متعبون ، ويجب أن نرتاح من حين لآخر ، لذلك لن أقرأ لك عشر بوصات كاملة ، ولكنني متأكد من أنني سوف أكون الحصول على أقرب ما يمكن أن نحصل عليه ، إلى أي مدى تعتقد أننا سوف نسافر؟
|
|
|
|
يمكنك أن تفكر هكذا:
|
|
|
|
* وأنا أعلم أنه بالنسبة لكل بوصة كنت تقرأ ، أقود 2 كيلومتر! لذا ، إذا كنت تميل إلى قراءة 10 بوصات ... همم ... ربما سنقترب قدر المستطاع لقيادة 20 كيلومترًا! ليس بالضبط ال 20 ، لكننا سنعمل على الحصول على وثيقة قريبة جدا.
|
|
|
|
هذه طريقة لتوضيح هذا المفهوم ، تخيل أنك تسير على الرسم البياني ، والوظيفة هي "القاعدة" ، و x هي "كم يجب عليك المشي" ، و f (x) هي القيمة التي تسلكها فعليًا ، القاعدة التي أعطيت لك.
|
|
|
|
#### الخصائص
|
|
|
|
ضع في اعتبارك أن حدود الوظائف موجودة ، ثم:
|
|
|
|
* **مجموع**
|
|
|
|

|
|
|
|
الحد الأقصى للمبلغ هو مجموع الحدود.
|
|
|
|
دع f (x) تساوي x ، f (x) = x و g (x) = 2x. دع x تميل إلى 1. الحد:
|
|
|
|
lim (f (x) + g (x)) = lim f (x) + lim g (x) = lim x + lim 2x = 1 + 2 = 3
|
|
|
|
أو lim (x + 2x) = lim (3x) = 3
|
|
|
|
* **المنتج**
|
|
|
|

|
|
|
|
الحد من المنتج هو نتاج الحدود.
|
|
|
|
خذ بعين الاعتبار نفس الوظيفة على المثال السابق ، f (x) = x و g (x) = 2x. وجعل x يميل إلى 2 ، الآن.
|
|
|
|
lim (f (x) \* g (x)) = lim f (x) \* lim g (x) = 2 \* 4 = 8
|
|
|
|
أو lim (x \* 2x) = lim (2x ^ 2) = 2 \* 4 = 8
|
|
|
|
* **المنتج من قبل ثابت**
|
|
|
|

|
|
|
|
يمكنك "عامل" ثابت مضاعف خارج الحد.
|
|
|
|
مرة أخرى ، افترض f (x) = x. الحد الأقصى ، نظرًا لميل x إلى 5 الآن:
|
|
|
|
lim (10 \* x) = 10 lim (x) = 50
|
|
|
|
lim (10x) = 50
|
|
|
|
* **قطاع**
|
|
|
|

|
|
|
|
الحد من التقسيم هو تقسيم الحدود.
|
|
|
|
دع f (x) = 2x و g (x) = x + 1. تأكد من أن الوظيفة التي ستنشئها ليست صفراً. جعل x يميل إلى 2 ، وكان لديك:
|
|
|
|
lim (2x / x) = lim 2x / lim x = 4/2 = 2
|
|
|
|
أو lim (2x / 2) = lim 2 = 2. هذه دالة ثابتة ، لذا بغض النظر عن مقدار ما تمشي عليه alonf ، فإن القيمة ستميل دائمًا إلى قيمة معينة واحدة.
|
|
|
|
* **قوة**
|
|
|
|

|
|
|
|
إذا كان n عددًا صحيحًا.
|
|
|
|
دع f (x) تساوي x + 1 والسماح x يميل إلى 2. افترض الحد التالي:
|
|
|
|
lim \[(x + 1)\] ^ 2 = (3) ^ 2 = 9
|
|
|
|
lim \[(x + 1)\] ^ 2 = lim (x ^ 2 + 2x + 1) = 9 (لاحظ أنه يمكنك استخدام خاصية sum أيضًا!)
|
|
|
|
#### معلومات اكثر:
|
|
|
|
[ملاحظات وأمثلة أخرى](http://tutorial.math.lamar.edu/Classes/CalcI/LimitsProperties.aspx)
|
|
|
|
[مقدمة للحد من محاضرة](https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-continuity/ab-limits-graphically/v/introduction-to-limits-hd) |